
Course Content
Formula Sheet
Example 1
A solid substance is placed in an insulated container and heated.
The graph shows how the temperature of the substance varies with time.
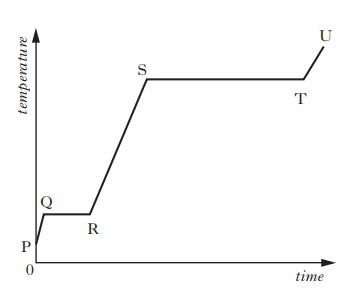
To calculate the specific latent heat of vaporisation of the substance, a student would use the time from section

We are asked for time we would use to calculate the specific latent of vaporisation.
This is when a liquid changes state into a gas.
When the gradient of the line is 0 (when the line is horizontal), the substance is changing state.
The substance is solid to start with. During section QR, the substance changes from solid to liquid.
During section ST, the substance changes from liquid to gas.
This means section ST would be used to calculate the specific latent hear of vaporisation of the substance.
So the answer is D
Example 2
The pressure of a fixed mass of gas is 150kPa at a temperature of 27°C
The temperature of the gas is now increased to 47°C
What is the pressure of the gas now?
We use the formula that relates pressure and temperature:
p1⁄T1 = p2⁄T2
We need to convert the temperature into Kelvin.
We do this by adding 273 to the temperature.
150 x 103⁄(27 + 273) = p2⁄(47 + 273)
p2 = 150 x 103 x (47 + 273)⁄(27 + 273)
p2 = 160 x 103 Pa
Example 3
A block has dimensions shown.

The block is placed so that one of the surfaces is in contact with a smooth table top.
The weight of the block is 4.9N
The minimum pressure exerted by the block on the table top is

This is a sneaky question. Notice how it says minimum pressure.
Lets think this through. Since:
p = F⁄A
For the smallest pressure, we needs the greatest area.
This means we need to use the surface with largest area.
p = 4.9⁄0.2 x 0.1
p = 245 Pa
So the answer is B
Example 4
An ice cream maker has a refrigeration unit which can remove hear at 120 J/s.
Liquid ice cream, of mass 0.6kg at a temperature of 20°C, is added to the container.
(a) Calculate how much energy must be removed from the mixture to cool it to its freezing point of -16°C.
(Specific heat capacity of ice = 2100J/kg°C)
(b) Calculate how much heat energy must be removed to freeze the ice cream at this temperature.
(Specific latent heat of fusion of ice cream = 2.34 x 105J/kg)
(c)(i) Calculate the time taken to cool and freeze the ice cream.
(c)(ii) What assumption have you made in carrying out this calculation?
(a) First we calculate the change in temperature to go from 20°C to -16°C.
ΔT = 20 + 16 = 36°C
Now we use the formula:
Eh = cmΔT
Eh = 2100 x 0.6 x 36
Eh = 45400 J
(b)We use the formula:
Eh = mlf
Eh = 0.6 x 2.34 x 105
Eh = 140400 J
(c)(i) First we need to calculate the total heat energy supplied:
Total Eh = 45400 + 140400 = 185800 J
Now we use the formula:
P = E⁄t
Note: Watts is also defined as Joules Per second. This means 120J/s is 120W
120 = 185800⁄t
t = 185800⁄120
t = 1550s
Example 5
A bicycle pump with a sealed outlet contains a certain volume of air.
The air inside the pump is at an initial pressure of a certain value.
The piston of the pump is now pushed slowly inwards, causing the volume of air in the pump to decrease. 2017 3B

Using the kinetic model, explain what happens to the pressure of the air inside the pump as its volume decreases.
This is some of the theory that you should know, as it is very common to get a question like this in the exam:
Since the volume decreases, the particles collide more frequently with the container walls than before.
This means there is a larger force acting on the wall, giving an increased pressure.
Example 6
A group of students are investigating how the pressure of a fixed mass of gas varies with its temperature.
This is know as Gay-Lussac's Law.
The students set up an experiment as shown.
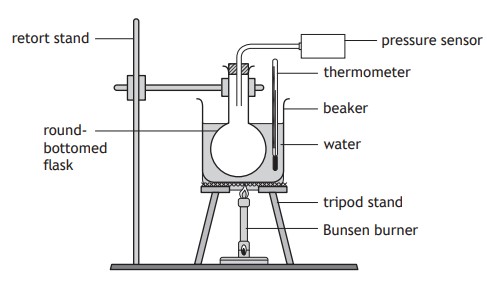
The round-bottomed flask contains a fixed mass of gas.
The Bunsen burner is used to heat the apparatus as shown.
Readings of temperature and pressure are taken every 10°C
During the experiment the volume of the gas in the round-bottomed flask remains constant.
The student's results are shown.
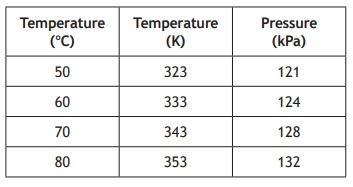
(a) Use all the appropriate data to establish the relationship between the pressure and the temperature of the gas.
(b) Predict the pressure of the gas at a temperature of 100°C
(c) Suggest one way the students could improve the experiment.
(a) This is a technique you should know to use, as this is a commonly observed exam question.
Before going into the exam, you should know the relationships between all the Gas Laws/potential relationships.
Here:
p ∝ T
Next, we re-arrange for a constant:
p ∝ T
p = Constant x T
p⁄T = Constant
Now, we use the formula for the constant for ALL of the values:
p1⁄T1 = 121⁄323 = 0.375
p2⁄T2 = 124⁄333 = 0.372
p3⁄T3 = 128⁄343 = 0.373
p4⁄T4 = 132⁄353 = 0.374
Now, we state that the formula equals a constant
e.g p⁄T = Constant of 0.374 (within experimental error)
Note: I used the mean value to determine a constant
Now, we re-arrange to prove that it's directly proportional.
p⁄T = Constant
p = Constant x T
therefore p ∝ T
(b) Here, we use the formula we used in the previous part to predict a value.
First, we need to convert 100°C to Kelvin. We do this by:
100 + 273 = 373K
Now we use the formula:
p⁄T = Constant
p⁄373 = 0.374
p = 0.374 x 373 = 140
Remember the units for pressure, and in this question, it is in kPa
p = 140kPa
(c) There are a range of things you could say. Examples include:
Repeat the experiment
Stir the water
Place the thermometer inside the flask